Casually Explained I: Positional Encoding in Transformers

Let’s talk about positional encoding in transformers over coffee! ☕️

Ever since the transformers were introduced in 2016, various transformer architectures have been used in solving many natural language processing (NLP) and computer vision (CV) tasks. Therefore, it is essential to understand the paper that started it all, “Attention Is All You Need”! Fortunately, there are many great blog posts out there that you can read and watch and I will link some of them at the end of the blog post.

In this blog post, we will focus only on positional encoding, which helps transformers keep track of the positions of the words in the sentences it takes input.

Whaat? Aren’t the input sentences in order already?

Yes, the transformers take groups of words in order, but they process them all at once. Recurrent neural networks, which were the most prominent machine learning algorithms for NLP tasks before transformers, processed the words in order and they were incredibly slow and very hard to parallelize, even with the computational advancements made in the last couple of years. Transformers, on the other hand, do not “care” about the order while processing and hence, are easy to parallelize. They have better memorization capabilities as well because self-attention makes all the steps available for the model at each step.

But then, wouldn’t they only learn a group of words, not sentences?

That is also correct! Then, they would not be able to translate sentences or generate meaningful text. Because, the order of the sentence without, we nothing have!¹ Transformers learn about the order of the sentences by using positional encoding.

Seriously, give me the scoop already!

Positional encodings are vectors that contain the position information of a word in a sentence. For each word, we use a d-dimensional vector to represent its position within the sentence. The values of the elements in the vector (which becomes a matrix if we compute for all words in the input sentence) will be determined according to the following function:

where pos is the position of the word within the sentence, i is the dimension within the positional encoding vector, and d_embed is the model embedding dimension. Simply put, the positional encoding vector for each word (embedding) is made up of alternating values of sines and cosines.

OK, but how do transformers use that info??

That’s straightforward, it’s just addition!

where WE is the word embedding matrix, and E is the final embedding matrix. With this step, all steps are completed!

Now, let’s visualize!

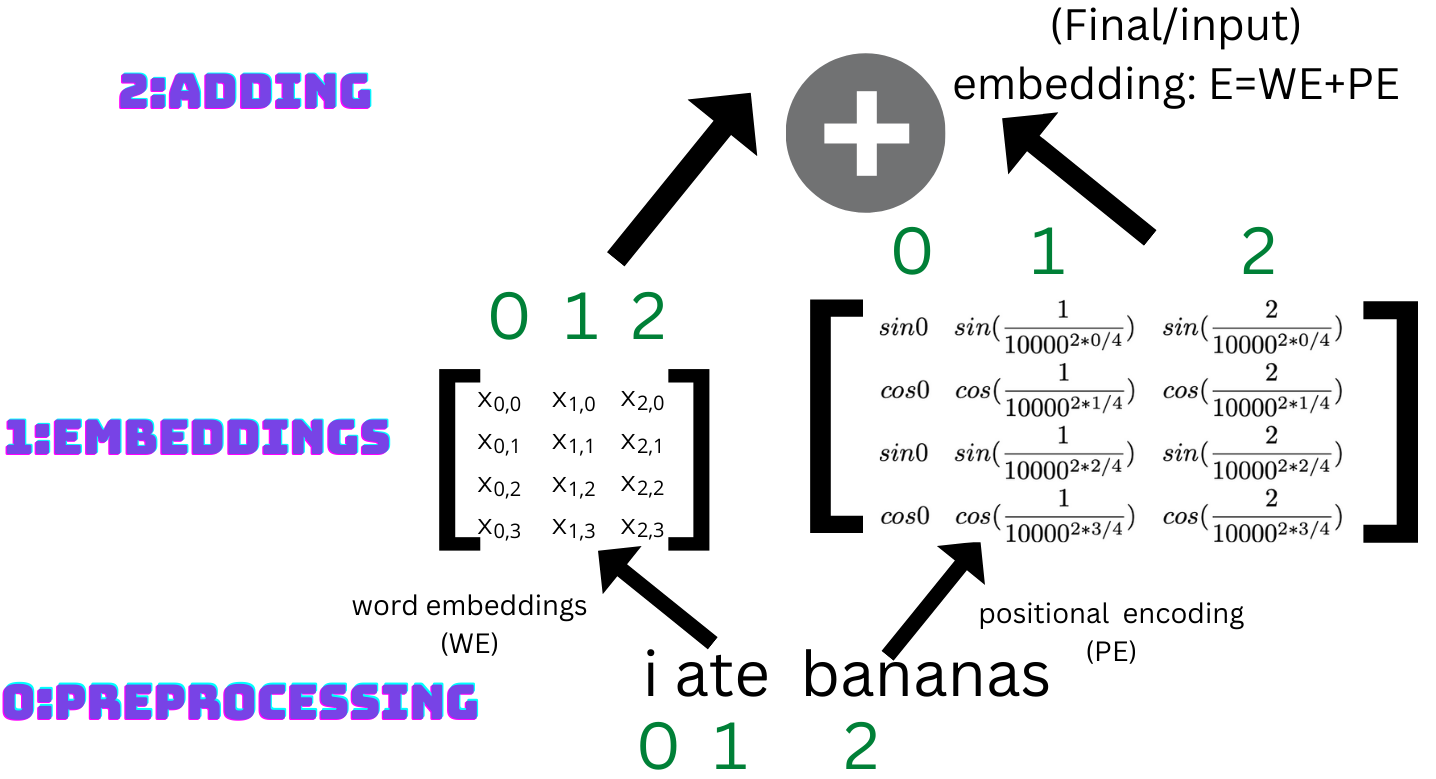
Below is a visual, detailing the embedding process as a whole in transformers, with an emphasis on how the positional encodings are computed.

First of all, the sentence possibly gets processed and transformed into another form, which we will talk about in another blog post. Then, the (choice of) word embeddings are computed. Afterward, the positional encodings are computed according to the formulas given in the previous section. Finally, the word embeddings and the positional encodings are added together and we have the input embeddings for our transformer!

Give me some code, plots, and intuition!

Here is the code for computing the positional encoding with size 500 for a sentence/word embedding of length 128.

import numpy as np

d_embedding = 500
pos_encs = np.zeros((128,d_embedding))

for pos in range(128):
    for i in range(int(d_embedding/2)):
        pos_encs[pos, 2*i] = np.sin(pos / (10000 ** ((2*i)/d_embedding)))
        pos_encs[pos, 2*i+1] = np.cos(pos / (10000 ** ((2*i)/d_embedding)))

That’s it because the content of the input sentence does not affect the content of the positional encoding matrix! Now, let us plot some parts of the pos_encs matrix and gain some intuition about why these numbers carry information about the positions of the words within the input sentences.

The blue line visualizes the values at the first row of the pos_encs matrix. The orange lines visualize the values at indices 10, 60, and 110 in order. Notice that the values represented by the blue line alternate between 0 and 1². Also, the values represented by the orange lines start off by oscillating in a more scattered/disorderly fashion and for larger embedding dimensions, they converge to oscillate between 0 and 1. As the index grows (the order of the word within the sentence increases), this "convergence" point is reached at a later dimension (column) within that row of the encoding matrix. This implies that the values generated by computing this particular positional encoding are unique for each word position in the sentence and that the positional encodings of words which are close to each other are more similar compared to ones that are farther apart. That's precisely what we want!

RESOURCES & RECOMMENDATIONS

1. https://jalammar.github.io/illustrated-transformer/

2. https://kazemnejad.com/blog/transformer_architecture_positional_encoding/

3. https://kikaben.com/transformers-positional-encoding/

4. https://towardsdatascience.com/illustrated-self-attention-2d627e33b20a

P.S. ☕️ I was drinking this coffee when I was writing this post and I would highly recommend it!

1. Because, without the order of the sentence, we have nothing! Even in this sentence, we have somewhat of an order.

2. which makes sense because the values computed alternate between sin0 and cos0.